Every time a quantum system undergoes a cyclic evolution ruled by a change of parameters, it acquires a section issue, often known as the geometric section. The commonest formulations of the geometric section are the Aharonov–Bohm section³ and the Berry section¹. Over the previous a number of many years, the geometric section has been generalized and have become notable in a number of functions—from condensed matter physics^4,5, fluid mechanics⁶ and optics^7,8 to particle physics and gravity⁹.

In condensed matter physics, the geometric section manifests within the digital Bloch states, main to varied observations such because the quantum Corridor impact, electrical polarization, orbital magnetism and trade statistics⁴. In these methods, making use of an electrical area drives the digital wavefunction within the crystal momentum area, resulting in the buildup of the Berry section due to the parameter area topology, and it is called Zak’s section when built-in over your complete Brillouin zone¹⁰. The native properties of this quantum evolution are captured by the Berry curvature, representing the native rotation of the wavepacket because it evolves throughout the Brillouin zone. The unique description of Berry’s section¹ required two basic situations. First, the section needs to be gathered as a quantum state evolves in a parameter area adiabatically. Second, the parameter needs to be modified repeatedly. A generalization of the Berry section^11,12 eliminated the adiabaticity requirement. Nevertheless, the sleek modification of the wavefunction in a steady parameter area, which underlies the essential mathematical formulations of the Berry section, varieties the principle a part of its numerous realizations¹³.

Right here we introduce and experimentally confirm a formulation of the geometric section, which incorporates each steady and discrete modifications of the wavefunction. This section, known as the interband Berry section, is pertinent to all light-driven quantum methods present process each adiabatic evolution and light-induced jumps within the Hilbert area. Experimentally, we give attention to the light-driven condensed matter methods. Pushed by a low-frequency exterior area, the digital wavefunction undergoes non-adiabatic interband transitions adopted by intraband propagation and, lastly, an extra non-adiabatic transition by photo-recombination. These dynamics type a closed loop within the power–momentum area (Fig. 1a). Though the evolution of the wavefunction in every band is steady, the light-induced transitions between the bands characterize a discrete evolution. The geometric section gathered alongside this closed path is gauge invariant¹⁴ measurable and performs an vital half within the response of a quantum system to an intense gentle area (see an in depth dialogue within the Supplementary Info).

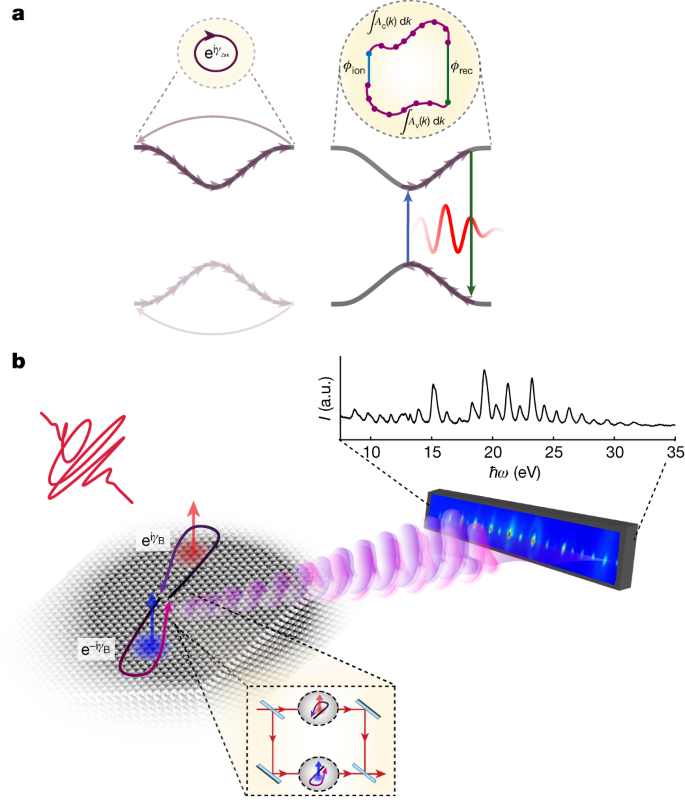
a, The Berry section in condensed matter methods. Left, intraband Berry section, gathered because the wavepacket, repeatedly evolves within the ok-space throughout the band. When the trajectory varieties a closed loop via your complete Brillouin zone, a gauge-invariant section is gathered (often known as the Zak section). Proper, interband Berry section, the wavepacket evolution contains discrete transitions between the 2 bands, closing a loop within the power–momentum area. b, HHG Berry-phase interferometry. An interferometric measurement is carried out by manipulating the instantaneous polarization of the laser area, producing two completely different wavepackets, evolving alongside the optimistic and the unfavourable half cycles. The interference sample is resolved within the HHG spectrum, encoding the relative gathered Berry section.

We resolve the interband Berry section¹⁵ by introducing attosecond interferometry, utilizing a polarization-controlled laser area to drive the evolution of the quantum wavefunction. Our scheme induces an inner interferometer within the ok-space by shaping the digital trajectories on a subcycle time scale, offering entry to the interband Berry section. By manipulating the instantaneous polarization of the laser area, we induce and management two completely different electron–gap paths, evolving in the course of the optimistic and unfavourable subcycles of the laser area. Their section distinction, recorded in a broken-inversion-symmetry crystal as a operate of laser area polarization, is resolved utilizing high-harmonic era (HHG) spectroscopy^16,17 (Fig. 1b). Pushed by the sturdy laser area¹⁸, the electron tunnels throughout the power hole between the valence and the conduction bands, initiating an electron–gap wavepacket¹⁹. This excitation is adopted by the propagation of the electron–gap wavepacket, dictated by the temporal form of the laser area, and electron–gap recombination, projecting the ok-space trajectories onto the emission of higher-order harmonics (often known as interband HHG)^20,21. The Berry section gathered by the electron–gap wavepacket is thus mapped onto the optical section and amplitude of the emitted harmonics. As numerous ok-space trajectories are projected onto completely different harmonics^22,23, this scheme can resolve the evolution of the Berry section over your complete Brillouin zone. Lastly, we acquire a direct perception into the native manifestation of the geometrical properties of the wavefunction, the Berry curvature^24,25,26,27, resolving its impression on the electron currents.

The first benefit of HHG spectroscopy lies in its time scale—your complete interplay evolves throughout lower than one optical cycle, avoiding scattering or dephasing occasions and preserving the coherence of the wavepacket^22,28. A earlier examine²⁵ confirmed the Berry curvature of topological insulators utilizing HHG pushed by THz area²⁹, having a basic interval of 40 fs. Of their examine, topology helps to beat dephasing and scattering mechanisms, exhibiting the geometrical properties of the system. Our measurement, carried out on an attosecond time scale, allows the probing of the Berry section in trivial insulators.

Formally, the gauge-invariant geometric section gathered throughout a cyclic evolution of the wavefunction within the power–momentum area will be evaluated as follows:

Right here (left|{u}_{n,{bf{ok}}}rightrangle ) is the periodic a part of the Bloch operate (n = v, c for valance and conduction bands), ε_g = ε_c − ε_v is band hole power and ({boldsymbol{mathcal{A}}}_{{rm{g}}}={boldsymbol{mathcal{A}}}_{{rm{c}}}-{boldsymbol{mathcal{A}}}_{{rm{v}}}) is electron–gap relative Berry connection ({boldsymbol{mathcal{A}}}_{n}({bf{ok}}),=)(({rm{i}}langle {u}_{n,{bf{ok}}}(x)| {nabla }_{{bf{ok}}}| {u}_{n,{bf{ok}}}(x)rangle )). The discrete evolution between the bands is described by the section of the interband dipole coupling, ({phi }_{{rm{d}}}({bf{ok}})=arg ({rm{i}}leftlangle {u}_{{rm{v}},{bf{ok}}}(x)proper|{nabla }_{{bf{ok}}}left|{u}_{{rm{c}},{bf{ok}}}(x)rightrangle )). The crystal quasi-momentum, ok(τ) = ok − A(t) + A(τ) is managed by the laser area, the place F(t) and A(t) are the laser electrical area and the vector potential, respectively. The instants t′ and t outline the transition occasions between the bands (the ionization and recombination occasions). The interband Berry section, γ_B,int, accommodates the evolution inside every band, described by the standard integral over the Berry connection, along with the section contributions related to the jumps between the bands, that are represented by the phases of the coupling dipoles. This Berry section represents a closed trajectory in power–momentum area and will be expressed as ({int }_{{{bf{ok}}}_{{rm{i}}}}^{{{bf{ok}}}_{{rm{f}}}}({boldsymbol{mathcal{A}}}_{{rm{c}}}({bf{ok}})-{boldsymbol{mathcal{A}}}_{{rm{v}}}({bf{ok}})){rm{d}}{bf{ok}}-({phi }_{{rm{d}}}({{bf{ok}}}_{{rm{f}}})-{phi }_{{rm{d}}}({{bf{ok}}}_{{rm{i}}}))). Recombination maps every closed trajectory into the emission of optical radiation, at a frequency of ε_g(ok(t)), projecting the Berry section, γ_B,int, onto the optical section of the emitted harmonics.

Interband Berry-phase interferometry

We extract the Berry section utilizing the sub-laser-cycle interferometric measurement. The 2 arms of the interferometer are the 2 electron trajectories, that are inverted with respect to one another and evolve in the course of the optimistic and unfavourable half cycles of the laser area (Fig. 1b). By controlling the instantaneous laser-field polarization, we management these trajectories within the ok-space and manipulate their interference. The management is achieved utilizing elliptically polarized gentle, which induces the two-dimensional (2D) movement within the ok-space. When the 2 trajectories evolve within the neighborhood of optimistic and unfavourable Berry curvatures, the gathered phases alongside the 2 arms could have reverse indicators (Fig. 2a). Rising the ellipticity, ϵ, allows us to repeatedly tune the 2D ok-space paths, and due to this fact the gathered Berry section. Lastly, the 2 emission bursts, related to the radiative recombination of the 2 trajectories, intrude within the HHG spectrum, encoding their relative section within the spectral form of the harmonics.

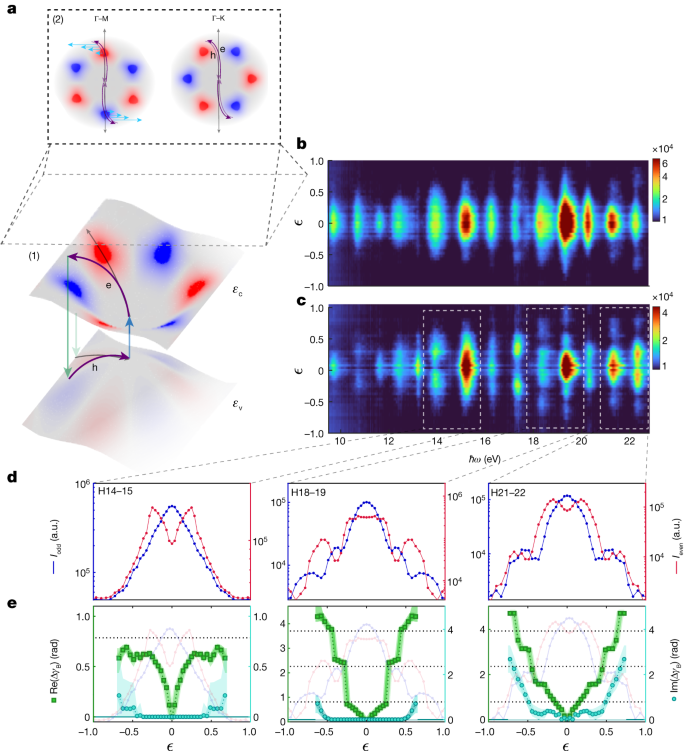
a, Schematic of the electron trajectories pushed by an elliptical area: (1) manipulating the laser ellipticity, ϵ, induces a transversal evolution of the electron–gap wavepacket, controlling the closed loop in power–momentum area. ε_v and ε_c correspond to the valance and conduction bands, respectively, colored in line with the Berry curvature (pink representing optimistic values and blue representing unfavourable values). Black arrows correspond to the trajectory induced by the linear driving area and purple arrows to the elliptical driving area; (2) a prime projection of the power–momentum area, ε_c − ε_v, illustrates the intraband wavepacket evolution alongside the Γ−M (30° crystal orientation) and Γ−Okay (0° crystal orientation). The sunshine-blue arrows characterize the Berry connection rising alongside the transverse evolution, resulting in the buildup of the Berry section. b,c, HHG spectrum (log scale) as a operate of the driving area ellipticity, resolved alongside the Γ−Okay (b) and Γ−M (c) axes. d, Odd (blue, left axis) and even (pink, proper axis) harmonic intensities as a operate of the ellipticity of the driving area, for harmonics (left to proper): H14–H15, H18–H19 and H21–H22. e, The reconstructed advanced Berry section, Δγ_B, as a operate of the ellipticity of the driving area for every pair of neighbouring harmonics (which are offered above, in d). We resolve each the true (inexperienced, left axis) and imaginary (cyan, proper axis) parts of the Berry section.

We experimentally exhibit the Berry-phase interferometry by producing HHG from an α-quartz z-cut crystal^24,30,31, utilizing a 1.2-μm laser area with an depth of order of 10¹³ W cm⁻². The harmonics spectrum spans as much as 30 eV, enabling us to probe the inner dynamics over a big power vary (Fig. 1b). By performing detailed theoretical and experimental research (Supplementary Info), we conclude that beneath our experimental situations, the interband mechanism dominates the harmonics emission. We be aware that this commentary is in distinction to the earlier commentary of HHG in quartz³⁰, carried out with shorter wavelength and laser pulses of few cycles.

Determine 2b,c presents the HHG sign as a operate of the driving area ellipticity (ϵ) alongside the Γ−Okay and Γ−M axes. Alongside the Γ−Okay axis, the harmonic sign decreases because the ellipticity is elevated (Fig. 2b). Owing to the rotation symmetry (C2) of the crystal alongside this axis, an electron trajectory, modified by the ellipticity of the sector, doesn’t accumulate an extra Berry section (Supplementary Info). On this case, as we improve the ellipticity, the transverse momentum will increase, resulting in the suppression of the electron–gap recombination. Rotating the crystal to the Γ−M axis results in a special response. Alongside this axis, rising the ellipticity decreases the odd harmonics sign and will increase the even harmonics sign (Fig. 2c). For prime ellipticity values, each the odd and even harmonics present fringe-like patterns oscillating out of section with one another (Fig. 2nd).

The oscillations of the HHG sign reveal the interferometric nature of the measurement. Each the odd and even harmonics end result from the interference of the alerts generated throughout two consecutive laser half cycles^32,33. This interference encodes the relative section gathered between the 2 closed quantum paths that the system takes throughout successive half cycles. To retrieve the section, we perturb the interferometric measurement by making the driving area weakly elliptic. We will then broaden the geometric section equation (1) to the primary order within the ellipticity of the sector, ϵ (Supplementary Info), resulting in the buildup of symmetric Δε_g(ϵ) and anti-symmetric Δγ_B(ϵ) parts. Within the presence of C2 symmetry, as is the case for the Γ−Okay course (or for any inversion-symmetric system), the perturbation is dominated by Δε_g, which is symmetric alongside the 2 interferometer arms. Rotating the crystal off this axis provides rise to the anti-symmetric contribution, Δγ_B(ϵ), which has an reverse signal alongside the 2 subcycles. Observe that the light-driven geometric section additionally contains an imaginary half, which captures the quantum nature of the interplay and is related to the contribution of the electron tunnelling throughout the band hole.

Lastly, the advanced perturbation is mapped onto the odd and even harmonics in line with (Supplementary Info):

the place ({{bf{E}}}_{0,N}^{pm }) are the unperturbed prefactors, containing the dipole couplings, akin to the interplay induced alongside optimistic and unfavourable half cycles. Because the measurement resolves the harmonic depth, solely the imaginary part of the symmetric a part of the perturbation Δε_g(ϵ) contributes, representing the suppression of the recombination chance with ellipticity. In contrast, the anti-symmetric section Δγ_B(ϵ) will be immediately noticed, inducing clear oscillations between the neighbouring odd and even harmonics. Alongside the Γ−Okay axis, through which the interplay is dictated by the C2 symmetry, Δγ_B(ϵ) = 0, and the interference is dominated by solely Δε_g (Supplementary Info). We discover that alongside this axis the even and odd harmonics present an identical response, decaying with the rising ellipticity. Resolving the interference alongside the Γ−M axis provides entry to Δγ_B(ϵ). As proven in equation (2), on this case we discover the alternative response of the odd and even harmonics with ϵ. This response serves as a delicate probe of this section, enabling its reconstruction.

Determine 2e presents the retrieved Berry section as a operate of the ellipticity of the driving area for harmonics H14–H15, H18–H19 and H21–H22. The reconstructed Berry section will increase with ϵ, following the bigger asymmetry induced by the elliptically polarized area (see Supplementary Info for an in depth description). Our reconstruction process is most correct at decrease ellipticity values. Furthermore, for greater harmonics, the reconstructed Berry section is bigger, reflecting longer trajectories related to these harmonics. The rise of the imaginary Berry section captures the quantum nature of the interplay, originating from each the tunnelling mechanism and the decreased electron–gap overlap with rising ellipticity. To the most effective of our data, that is the primary experimental commentary and reconstruction of the interband Berry section in crystals, resolved by strong-field light-matter interactions.

Resolving the Berry curvature

Subsequent, we lengthen our interferometry scheme to probe the well-known native geometrical property, the intraband Berry curvature (({boldsymbol{Omega }}={nabla }_{{bf{ok}}}occasions boldsymbol{mathcal{A}})). Though the Berry section and the Berry curvature are strongly associated, their bodily properties are inherently distinct, resulting in completely different observations (Supplementary Info). The intraband Berry curvature provides rise to a big number of phenomena, equivalent to Corridor conductivity and orbital magnetism⁴. Specifically, the applying of an electrical area induces a transverse present, regular to the Berry curvature course, related to the anomalous velocity (({{bf{v}}}_{{rm{an}}}=-frac{e}{hbar }{bf{F}}occasions {boldsymbol{Omega }}), the place F is the electrical area). The anomalous velocity induces a drift of an electron trajectory within the lateral course within the coordinate area (Fig. 3a), whereas its ok-space trajectory stays unchanged. The HHG mechanism serves as an especially correct probe of the Berry curvature due to the lateral drift it induces¹⁴. This drift suppresses the spatial overlap between the electron and the outlet, suppressing the recombination chance and due to this fact the HHG sign (Supplementary Info). Earlier research resolved the Berry curvature utilizing HHG polarimetry, dictated by all parts of the interplay—the intraband evolution in addition to the dipole couplings^24,25,26. In contrast, our measurement scheme gives a direct native probe of the anomalous velocity, isolating its impression on the light-driven trajectories.

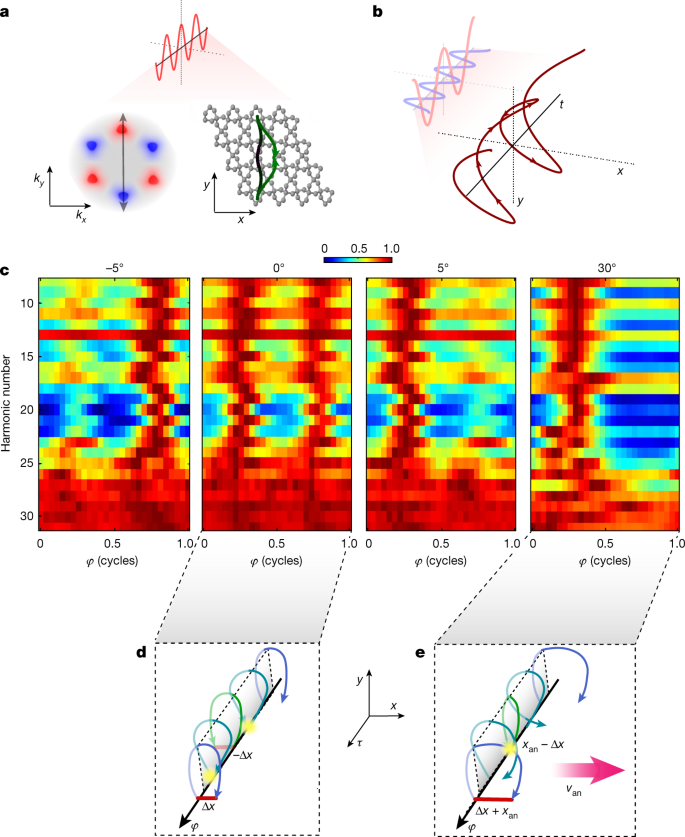
a, Intraband wavepacket evolution, in momentum (left) and actual (proper) area, induced by a linearly polarized area (darkish inexperienced to gentle inexperienced, representing the evolution in time from the tunnelling time to the recombination time). The trajectory within the prime and backside planes corresponds to the optimistic and unfavourable half cycles of the driving area, respectively. b, Time evolution of the two-colour orthogonally polarized area. The basic area is polarized alongside the y-direction and its second harmonic area alongside the x-direction, for a case of zero subcycle delay (φ = 0) between the 2 fields. c, The harmonics sign as a operate of the two-colour delay (φ), resolved for various crystal orientations (left to proper: −5°, 0°, 5° and 30°). Every row within the 2D plot is normalized by its maximal worth. d,e, Schematic of real-space wavepacket evolution, in the course of the basic first subcycle, for various time delays between the 2 fields. The lateral displacement of the electron–gap wavepacket on the recombination time (Δx) is induced by the two-colour area, through which the maximal and minimal harmonic alerts are achieved on the minimal and most displacement, respectively (yellow marker). The lateral shift induced by the anomalous velocity is represented by x_an.

In a broken-inversion-symmetry crystal, the Berry curvature inverts its signal between ok and −ok. Subsequently, when the interplay is pushed by a single-colour area, an equivalent lateral drift is induced between the 2 consecutive half cycles, producing two mirror-imaged real-space paths (Fig. 3a). We present the function of the Berry curvature by driving the interplay with a laser area that holds the identical mirror-symmetry property. This symmetry is achieved by combining the elemental area with its orthogonally polarized second harmonic³⁴. The whole vector potential rotates in a 2D airplane (Fig. 3b), inducing two mirror-imaged trajectories. This manipulation modifies the evolution of the wavefunction in a controllable method—enhancing or compensating the anomalous velocity and the related drift. Controlling the delay between the 2 fields, φ, shapes the instantaneous 2D laser area, driving the electron alongside or towards the anomalous velocity course. This manipulation suppresses or enhances the recombination chance and is immediately mapped onto the HHG sign. Importantly, owing to symmetry, the ok-space interferometer is balanced, through which the relative interband Berry section cancels out. This scheme allows us to isolate the function of the Berry curvature and seize its direct affect on the electron trajectories.

Determine 3 experimentally resolves the function of the intraband Berry curvature on laser-driven electron trajectories. Determine 3c presents the harmonic sign as a operate of the two-colour delay, φ, measured at completely different crystal orientations²⁴. First, we give attention to the Γ−Okay course (0°), having a C2 symmetry, through which the Berry curvature is zero. When the interplay is pushed by a single-colour area, the electron–gap follows a one-dimensional trajectory. The addition of a weak second harmonic area induces 2D mirror-symmetric trajectories having a lateral shift (Fig. 3d, pink line, Δx), through which the interplay can not distinguish between the left- or right-lateral displacement. This case is equal to an inversion-symmetric crystal, through which zero lateral shift is obtained twice inside one interval of the second harmonic area. Determine 3c reveals this periodicity, figuring out the elemental symmetry of the interplay and the absence of the Berry curvature. A delicate rotation of the crystal, by simply 5°, dramatically modifications this commentary, lowering the periodicity of oscillations to be a full cycle of the second harmonic area. As soon as the Berry curvature turns into non-zero, a small displacement is induced because of the anomalous velocity (Fig. 3e, x_an), driving the electrons alongside 2D mirror-symmetric paths. Right here the addition of the second harmonic area identifies the function of the anomalous velocity, compensating or rising the induced lateral drift. On this case, the full drift alongside the correct or left course turns into distinguishable. We maximize the symmetry breaking by rotating the crystal alongside the Γ−M axis (30°), maximizing the Berry curvature itself. On this case, there is just one delay through which each contributions—the anomalous velocity and the second harmonic area—compensate one another, lowering the periodicity of the measurement to be one second harmonic interval. These outcomes establish unequivocally the dominant function of the Berry curvature within the evolution of strong-field-driven electrons.

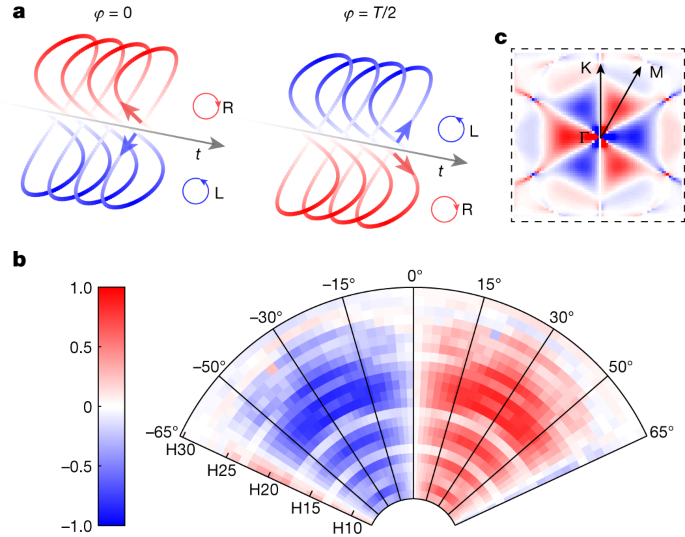
The 2-colour HHG scheme varieties a singular configuration, enabling the detection of the Berry curvature in a time-reversal symmetric system. The excessive sensitivity is supplied by the extremely nonlinear nature of the interplay; the response in the course of the first half cycle is localized round Γ−M (optimistic Berry curvature) and in the course of the second half cycle round Γ−M′ (unfavourable Berry curvature). Importantly, though the general laser area is just not chiral, the instantaneous chirality of the sector modifications its course between two consecutive half cycles³⁵ (Fig. 4a). As we shift the two-colour delay by T/2 (T is the second harmonic interval), we reverse the instantaneous chirality. Subsequently, the sign distinction between these two delays displays a round dichroism (CD) measurement: ({{rm{CD}}}_{{rm{HHG}}}equiv frac{I(varphi )-Ileft(varphi +frac{T}{2}proper)}{I(varphi )+Ileft(varphi +frac{T}{2}proper)}). In Fig. 4b, we plot the round dichroism sign, resolved for various harmonic numbers, as a operate of the orientation of the crystal. As will be noticed, alongside Γ−Okay (0°) the round dichroism sign vanishes, having its largest values across the maximal Berry curvature (Γ−M, 30°). Furthermore, in distinction to the well-known linear optical schemes, the round dichroism sign measured by this scheme is extraordinarily excessive, approaching 70%. The excessive sensitivity is supplied by the strong-field nature of the interplay, reflecting its exponential dependence on the Berry curvature (Supplementary Info).

a, The instantaneous chirality of the two-colour area, managed by the two-colour delay configuration, reversing its signal between consecutive half cycles. b, Experimentally resolved HHG round dichroism, CD_HHG, anti-symmetrized alongside 0° orientation (Supplementary Info), as a operate of harmonic order (radial axis) and crystal orientation (azimuthal axis). c, The DFT-calculated Berry curvature of one of many conduction bands, Ω₁₆, representing the origin of the HHG round dichorism, dictating its symmetry properties.

In abstract, our examine presents a beforehand unknown formalism of the Berry section, gathered in each discrete and steady area. HHG spectroscopy allows us to understand Berry-phase interferometry and probe the coherent properties of electron–gap wavefunction on a subcycle time scale. We experimentally exhibit this scheme and resolve the generalized Berry section throughout a big power vary. Extension of the strategy to a two-colour area allows delicate probing of the Berry curvature. The power to resolve angstrom-scale displacement of the electron enhances the sensitivity of the measurement by orders of magnitude, enabling us to probe extraordinarily low values of the curvature. We imagine that the elemental properties of our measurement will place HHG spectroscopy as a singular experimental scheme to establish Berry curvature and topological phases at greater conduction bands³⁶. Importantly, this scheme gives alternatives for Berry curvature measurements in insulators, probing a wide range of condensed matter methods that can’t be resolved utilizing transport measurements⁴ or different methods. Lastly, our scheme opens new paths in probing light-driven band construction, through which the elemental properties of the stable change throughout lower than one optical cycle³⁷, exhibiting attosecond-scale topological phenomena^25,38.